
最新文章
深圳市多中心空间结构的协同性测度研究
2024-05-30摘要
文章基于中心度、功能联系性和集聚水平指标,建构多中心城市空间结构的协同性测度框架,并以深圳市为例进行实证研究。文章认为,深圳市多中心空间结构呈现出网络化发展趋势,主要城市中心的集聚能力得到持续强化,外围组团的独立性呈现增强趋势,枢纽型节点的重要性逐渐凸显。通过功能联系性、集聚水平指标,测度各中心之间的联系程度、要素流动关系,评价各中心的集聚能力,进而测度多中心城市空间结构的协同性,是一种全面体现功能联系性和空间集聚度特征的综合测度方法,对测度超大、特大城市内部多中心空间结构的协同性,具有较好的理论和实践指导意义。
作 者
赵广英 哈尔滨工业大学(深圳),高级工程师
宋聚生 哈尔滨工业大学(深圳)建筑学院执行院长、教授
朱继任 哈尔滨工业大学(深圳)建筑学院城市规划系副主任、助理教授(通讯作者)
在城市研究领域,多中心(Polycentricity)既可以表示城市之间的集聚网络状态,也可以表示城市内部的多核结构,包括形态多中心、功能多中心及行政管理多中心等,多侧重于空间和功能的联系。对于超大、特大城市而言,过去几十年里,社会、经济空间结构的网络趋势得到持续强化,城市空间结构趋于多中心化,单中心模型难以准确地描述城市空间结构。
学界关于城市多中心结构的研究多关注其对促进职住平衡、提高土地利用效率、提升交通组织效率等方面的积极意义,如对芝加哥、悉尼、巴塞罗那、北京、上海等都市区多中心空间模型的研究。近年来,部分学者关注大数据与城市多中心结构的测度,如集中性的测度方法、中心等级与均衡性的测度方法,以及网络联系、通勤流、引力模型等功能联系方面的测度方法。少量学者还从网络结构方面研究多中心城市的协同性。
总体而言,在开放、流动的城市系统中,关于区域、城镇群空间协同性的研究十分丰富,既有研究关注的重点多集中在都市圈、都市区层面,鲜有针对多中心城市内部空间结构协同性的研究。从城市尺度解析各部分的空间结构关系,通过量化实证的方式测度其协同性,有进一步研究的必要。因此,本研究聚焦深圳市多中心空间结构的协同性问题,关注超大、特大城市内部空间结构的协同关系,试图建构相应的测度框架。
01
提出问题
尽管多中心城市空间结构的测度领域已有丰富的研究成果,但仍存在诸多不足。第一,在既有研究中,城市中心的识别结果容易受分析尺度影响,且修正系数的设定存在主观性,分析粒度的大小也会直接影响测度结果;第二,在既有研究中,城市往往作为一个节点统计,容易受行政区划面积影响,这与开放市场环境下超大、特大城市实际的空间结构不相符;第三,测度目标存在差异,形态上的多中心不代表功能上的多中心,测度范围变化会对结果产生巨大影响。对于超大、特大城市而言,行政区划带来的空间边界趋向模糊化,城市内部的诸多职能中心、重要的功能平台及特色功能区,往往在区域网络中扮演重要角色,其重要性并不逊于一般意义上的城市。
因此,研究关注超大、特大城市内部空间结构的协同性测度,基于熵指数(Entropy Index)、泰尔指数(Theil Index)综合测度城市中心度,识别潜在的城市中心,淡化行政区划的影响。综合相对引力模型(Gravity Model)、强度系数(Relative Strength Index)、局部莫兰指数(Local Moran's I)等多种方法,校正各中心的功能联系性;结合节点对称系数(Node Symmetry)、皮尔逊相关系数(Pearson Correlation)等方法,校验各中心的集聚水平,弥补单一测度方法造成的失真问题。
02
测度方法的理论建构
2.1 理论建构逻辑
研究从中心区的识别和中心之间的协同性测度两个层面搭建理论框架。在中心区识别方面,研究淡化建立在行政区划基础上的中心体系,运用POI(Point of Interest)熵指数算法,测度基于商业网点的栅格中心度;考虑到“市—区—组团—街道”等多层级服务设施密度的差异,运用泰尔指数的方法,对中心度的测度结果进行修正;进而运用阈值法,提取城市主要的中心区域,划定各中心的腹地范围。在中心之间的协同性测度方面,分别测度各中心之间的功能联系性和集聚能力,以体现多中心结构的差异。功能联系越紧密,集聚能力越强,表示该中心越重要。一方面,选用相对引力模型、强度系数、局部莫兰指数等多种方法,测度各中心的功能联系性。引力模型体现各中心经济、人口体量的相对影响力;强度系数体现各中心工作通勤的联系强度差异;局部莫兰指数体现联系高值、低值的空间集聚特征,三者加权叠加,反映各中心之间功能联系性的差异。另一方面,通过节点对称系数、皮尔逊相关系数的方法,测度各中心的集聚能力。节点对称系数能够反映节点之间交通联系的单向集聚能力;皮尔逊相关系数能够体现交通出行与经济体量的相关性,用来校验各中心集聚水平与中心职能的匹配程度,通过加权求和的方式,反映各中心的空间集聚能力(图1)。
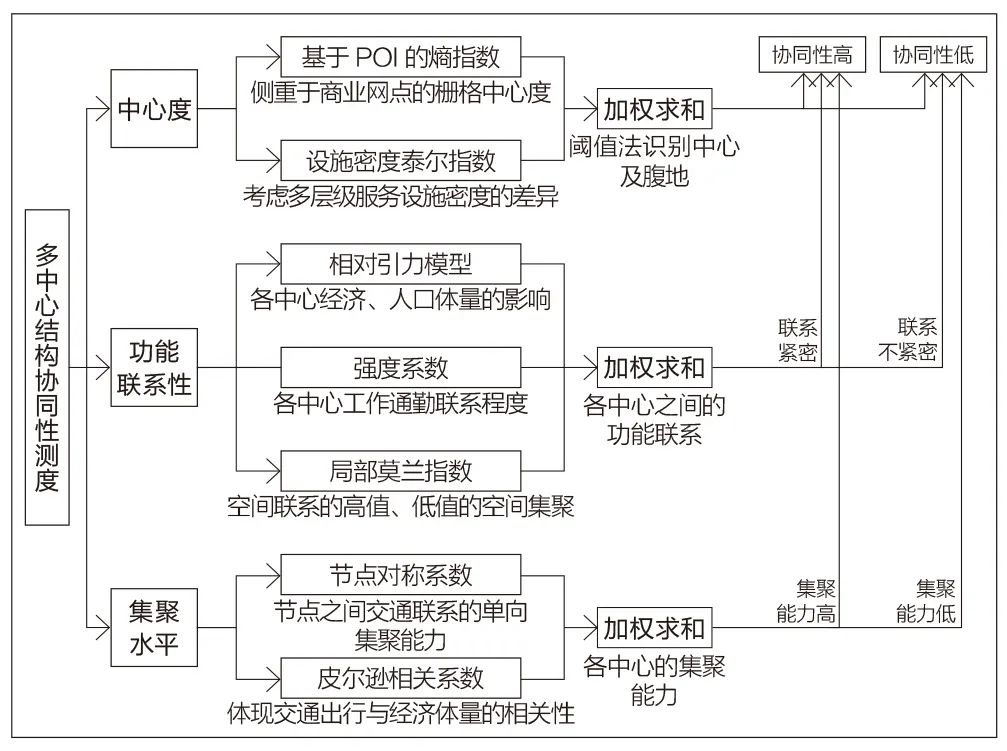
图1 多中心空间结构协同性测度的理论框架
Fig.1 A theoretical framework to measure the synergy of the polycentric spatial structure
资料来源:笔者自绘
2.2 研究对象、数据
2.2.1 研究对象
作为中国改革开放后崛起的速生城市(用40年时间走完国外大都市上百年的城市化历程),深圳市2000年后开始面临土地空间资源紧约束,步入转型发展阶段,城市空间形态逐步由带状组团向多中心网络转变。深圳市通过城市空间结构的优化调整,动态地适应外部市场环境变化,形成典型的超大城市多中心空间结构演变路径。研究深圳市多中心城市空间结构的协同性特征及其演变过程,对正在或即将面临多中心化趋势的其他城市具有借鉴价值。
2.2.2 研究数据
研究使用深圳市2019年10月14日6∶00—24∶00(工作日)出租车的定位数据(原始数据隐去具体日期和用户ID),测度城市中心之间的功能联系性,评价城市中心的集聚水平。考虑到以出租车数据为点位数据,需要投影并对相同ID的起、止点数据进行提取,该数据量达90余万条,且在原特区内外分布相对均衡,虽然无法避免分摊率低的问题,但用于分析高峰时段的通勤情况仍具有代表性。同时,研究获取高德地图2019年10月14日的兴趣点POI数据,该数据超过110万条,在全域范围内覆盖良好,可用于测度市域范围内各渔网(200m×200m栅格)的中心度,识别各中心的空间范围。
2.3 测度模型及变量
本研究首先使用熵指数、泰尔指数,分别测度全市范围内各渔网的中心度,识别各中心的实体范围,判断潜在的中心区域;其次,通过功能联系性分析,测度各中心之间的联系程度、要素流动关系,探讨各中心之间的协同关系;最后,通过集聚水平指标分析,测度各中心集聚能力的差异(表1)。
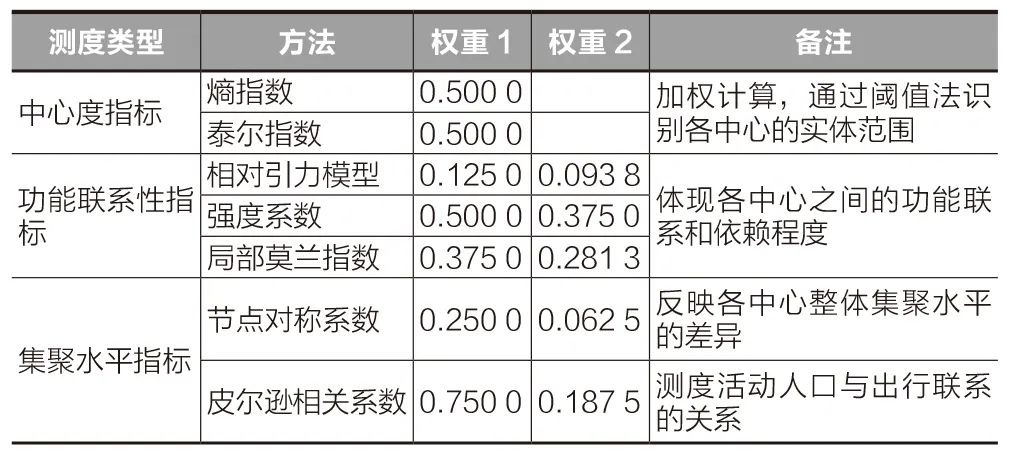
表1 协同性测度模型及权重
Tab.1 Measurement model and weight of synergy
注:表中权重1、权重2基于AHP层次分析法(和积法)计算,权重1为测度类型内部权重;权重2为功能联系性、集聚水平指标两种测度类型的整体权重。
资料来源:笔者自绘
2.3.1中心度测度
中心度使用熵指数、泰尔指数 分别进行测度,体现各中心发展水平和相应的集聚特征,通过阈值法识别各中心的实体范围。研究基于POI数据的熵指数,测度200m×200m粒度的渔网内各类型POI的集聚程度。同时,考虑各渔网内“市—区—组团—街道”等各级服务设施数量的密度差异,运用泰尔指数法对其进行修正,加权求和得到各渔网中心度的测度结果。通过阈值法,提取5%的区域聚合面,标记为城市中心或潜在中心区,进行泰森多边形邻域分析,获取各中心大致的服务区范围,同时结合街道级行政区划,得到全市各中心的腹地范围。
熵指数计算公式如下:
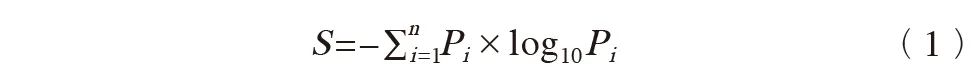
式中,n为渔网数量;Pi为渔网i中各大类POI数量占总POI数量的比例;S为熵指数,取值范围为[0,1],S值越接近1,表示空间集聚程度越趋于均衡,反之,则表示呈明显的中心集聚性。
泰尔指数计算公式如下:
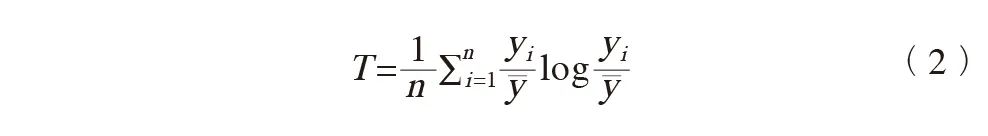
式中,yi为渔网i的服务设施密度;y为各渔网服务设施密度的平均数;n为渔网数量;T为泰尔指数,取值范围为[0, 1],T值越小,表示水平差异越小,反之,则表示中心性越强。
2.3.2 功能联系性测度
功能联系性测度使用引力模型、相对强度系数、局部莫兰指数等方法,对各中心之间的功能联系性进行测度,体现各中心之间的功能联系性和依赖程度。
首先,基于POI密度测度各中心之间的引力。参考郭建科、焦世泰、温馨、刘庆芳等对引力模型系数的修正,有如下计算公式:
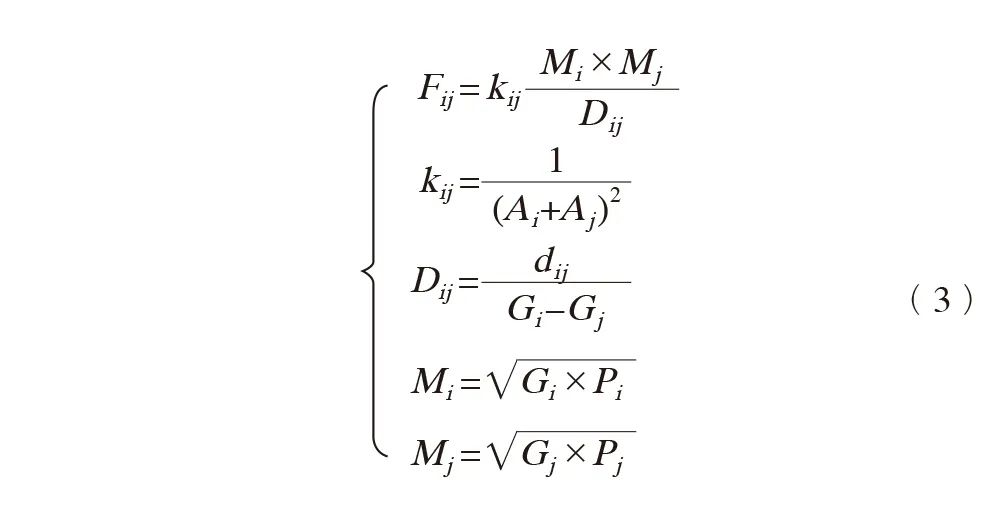
式中,Fij为中心i与j之间的引力,值越大,表示相应的空间依赖性越强,结构协同性越强;Gi、Gj分别为中心i、j的POI总数量;Pi、Pj分别为中心i、j的公共服务设施总数量;dij为中心i与j的空间距离;Ai、Aj分别为中心i、j的腹地面积。
其次,运用上班时段(7∶00—9∶00)的载客出租车数据,识别其运行轨迹,提取各中心出租车数量和跨中心流动出租车数量。使用相对强度系数,测度各中心之间的通勤流量。运用局部莫兰指数模型,评价各中心之间的集聚程度。
相对强度系数计算公式如下:
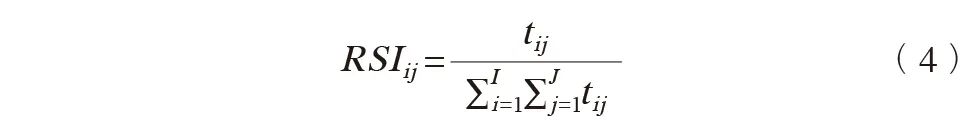
式中,RSIij 为相对强度系数,取值范围为[0, 1],值越大,表示联系越紧密;tij为中心i到中心j的出租车出行数量,i=1, 2, 3, …, I;j=1, 2, 3, …, J;i≠j。
局部莫兰指数计算公式如下:
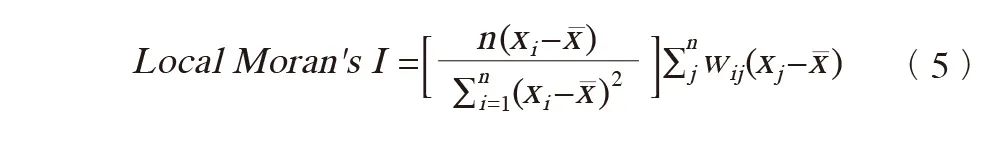
式中,Moran's I的取值范围为[-1, 1],取值为正,表示正自相关,即高值与高值集聚,低值与低值集聚的状态;取值为负,表示负自相关,即高值与低值相邻;取值趋近于0,表示不存在集聚特征。n为中心个数;xi为中心i的活动出租车数量;xj为中心j的活动出租车数量;x为各个中心的平均活动出租车数量;wij为中心i、j之间的空间权重,用距离平方的倒数表示。
最后,将引力模型、相对强度系数、局部莫兰指数的测度结果统一量纲,标准化后加权求和,得到各中心之间功能联系程度的测度结果。
2.3.3 集聚水平测度
本研究使用节点对称系数,分析各中心向心、离心出行差与出行总量的比例,评价各中心的单向依赖程度。使用皮尔逊相关系数,测度经济活动(POI数量或密度)与出行联系的相关性,反映各中心整体集聚水平的差异。统一量纲后进行加权求和,得到各中心的集聚能力。
节点对称系数计算公式如下:
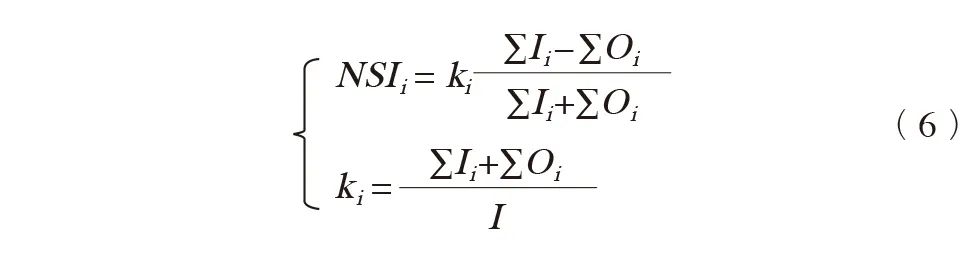
考虑各中心出行总量差异巨大,需要体现两个中心在城市整体出行量中的份额,研究引入修正系数ki。式中,NSIi为节点对称系数,取值范围为[-1, 1],值趋近于0,表示完全对称;值趋近1,表示向心集聚能力强,反之,则表示呈离心化状态。Ii为中心i向心出行的数量;I为城市出行总量;Oi为中心i离心出行的数量。
皮尔逊相关系数计算公式如下: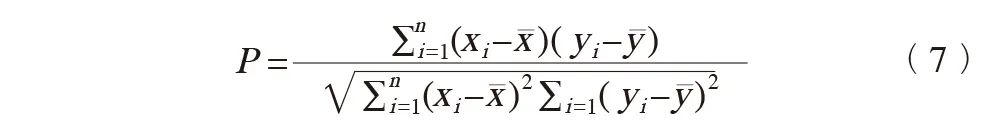
式中,P为皮尔逊相关系数,取值范围为[-1, 1],绝对值趋近于1,表示两个因素呈直线方程关系;绝对值趋近于0,表示两者不具有线性关系。n为中心个数;xi为中心i的活动出租车数量;yi为中心i的POI数量;x、y分别为xi、yi的平均数。
2.3.4 结构协同性测度
城市整体结构协同性分别测度城市各中心的功能联系性与集聚水平,进行加权求和,计算各中心的协同性。
城市结构协同性计算公式如下:
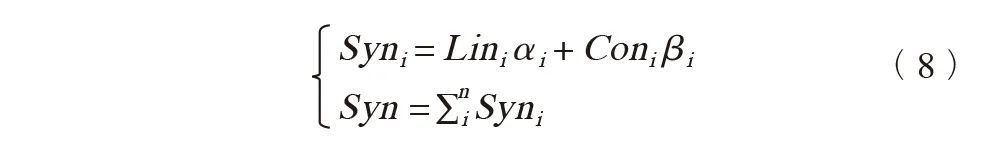
式中,n为城市各级中心的个数;Syn为城市结构协同性;Syni为中心i的结构协同性,Lini为中心i的功能联系性,Coni为中心i的集聚性;Lin、Con的测度结果需要分别进行标准化;α、β分别代表对应的权重。
03
结果与分析
3.1 协同性测度结果
3.1.1 多中心结构识别
熵指数、泰尔指数的综合测度结果表明,深圳市呈现出多中心的城市空间结构,除罗湖、福田、南山、前海等全市性的中心以外,还存在龙岗、龙华、宝安北、布吉、坂田、光明等规模较大的中心。此外,在横岗、平湖、石岩、莲塘、盐田、坪山、大鹏等区域,还形成大量潜在的中心。通过5%的阈值,提取具有统计显著性的峰值,识别出17个主要中心的实体范围,各中心呈现连片聚合的态势(图2、图3)。
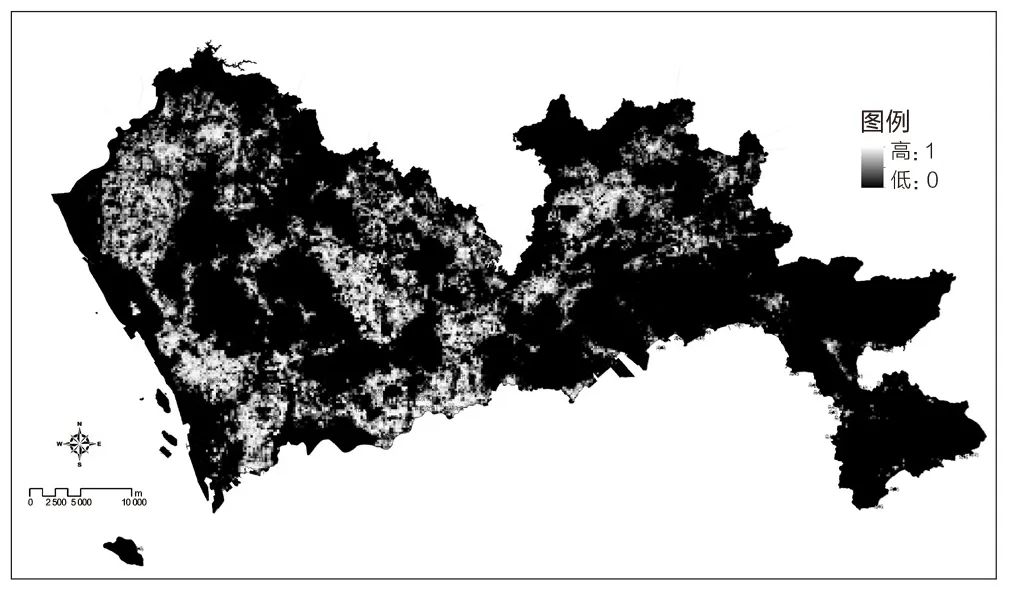
图2 中心度的测度结果
Fig.2 Results of the centrality measure
资料来源:笔者自绘
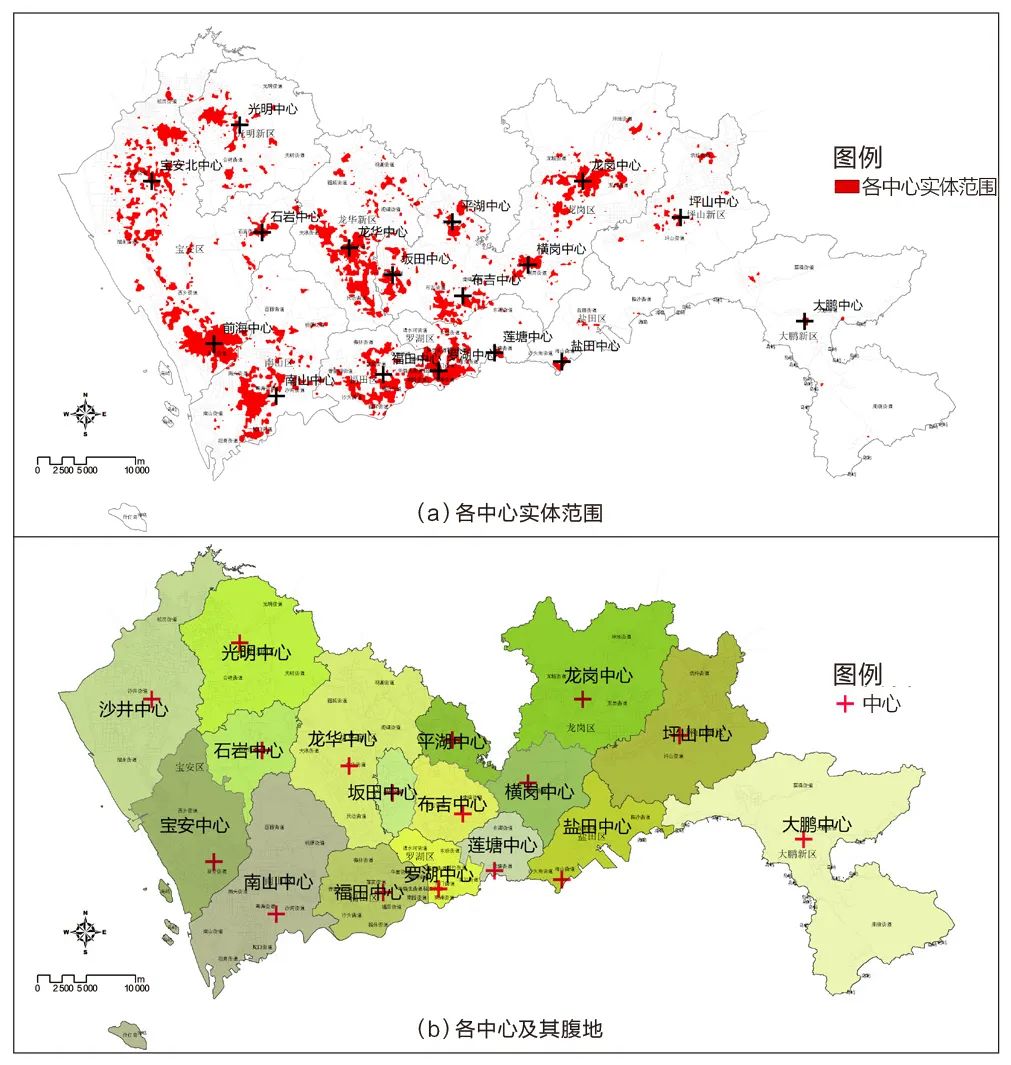
图3 中心及中心腹地的识别
Fig.3 Identification of center and central hinterland
资料来源:笔者自绘
3.1.2 中心之间的功能联系性
基于17个主要的中心节点,建构点距离空间联系模型。运用引力模型、相对强度系数、局部莫兰指数等方法,对各中心之间的功能联系性进行测度。
从引力模型的测度结果来看,罗湖—福田、龙华—坂田、罗湖—布吉、罗湖—坂田、福田—坂田、布吉—坂田、坂田—平湖等节点之间的联系较强,其次是南山—前海、南山—福田、布吉—横岗、罗湖—莲塘、福田—布吉、平湖—布吉等,中部各中心的引力相对较大(图4)。相对强度系数的测度结果表明,罗湖—福田、福田—南山、福田—前海、南山—前海等中心的联系最强,其次是福田—龙华、福田—布吉、罗湖—布吉、罗湖—莲塘、龙华—坂田等,相对联系强度集中在南部各中心之间(图5)。局部莫兰指数的测度结果显示,罗湖、福田、南山、前海节点之间联系紧密,位于第二梯队的龙华、布吉、坂田、莲塘与主中心联系紧密,但与其他中心之间的联系较弱(图6)。
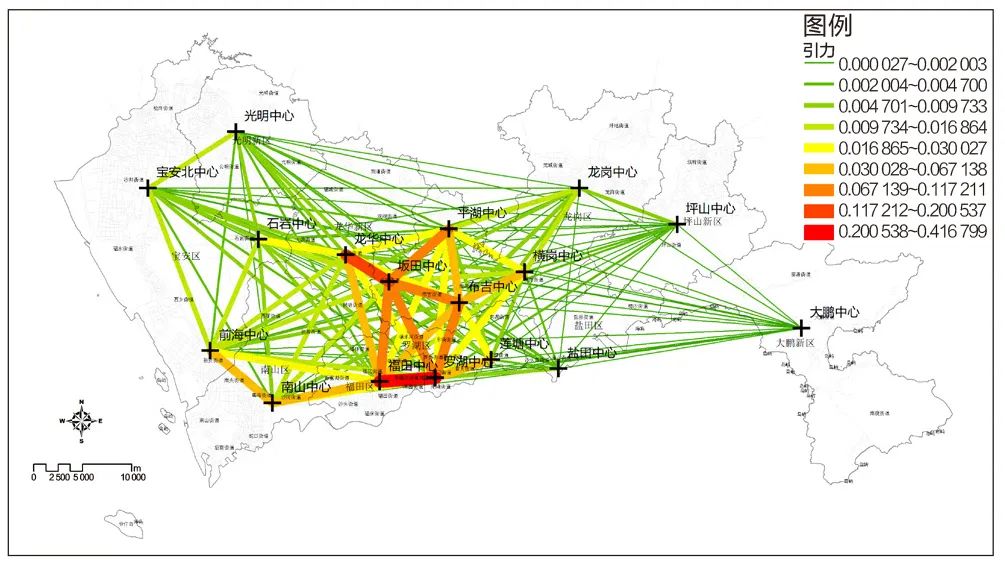
图4 各中心之间的引力
Fig.4 Gravitational force between centers
资料来源:笔者自绘
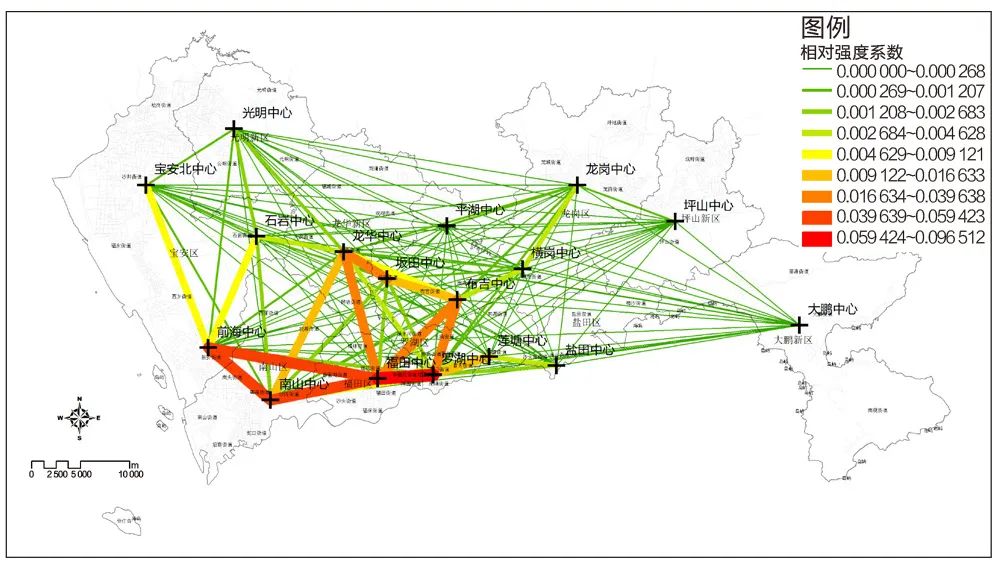
图5 各中心之间的相对强度系数
Fig.5 Relative strength index between centers
资料来源:笔者自绘
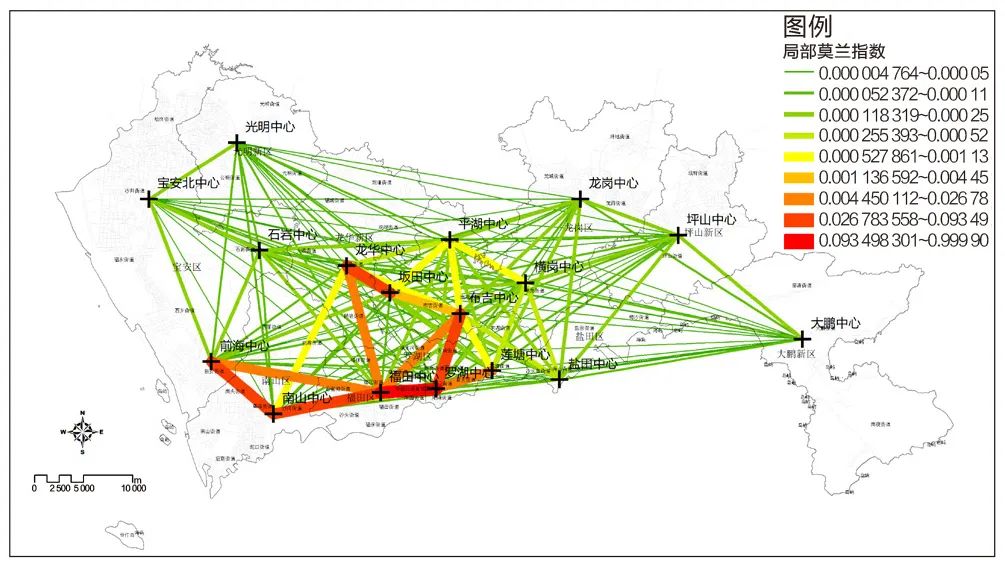
图6 各中心之间的局部莫兰指数
Fig.6 Local Moran's index between centers
资料来源:笔者自绘
综合引力模型、强度系数、局部莫兰指数等测度结果,标准化后进行加权求和,测度城市各中心的功能联系性。结果表明:第一,罗湖、福田、南山三个主中心与各中心之间的联系最为紧密;第二,前海中心与南山、福田中心的联系紧密,龙华中心与坂田、福田中心的联系紧密,布吉、龙华、坂田、横岗等区域性中心之间存在较强的联系;第三,宝安北、龙岗、盐田等传统意义上的组团中心与城市主要中心之间的联系较弱;第四,宝安北、光明、龙岗、坪山、大鹏等外围中心之间的联系较弱,呈现向心性(图7)。
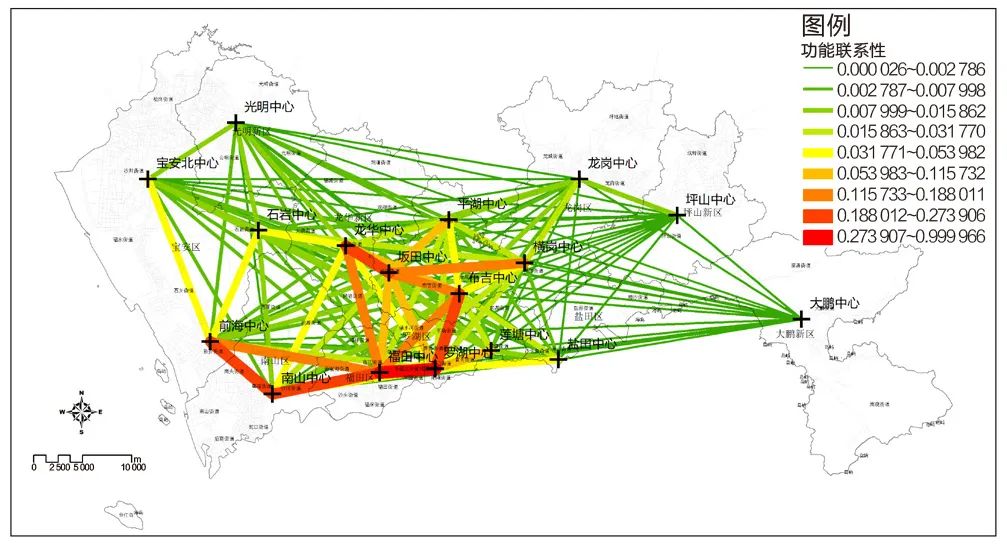
图7 各中心之间的功能联系性
Fig.7 Functional connectivity between centers
资料来源:笔者自绘
3.1.3 各中心的集聚水平
结合节点对称系数的测度结果看,罗湖、福田、南山、龙华、前海等中心的向心性较强,是城市主要的就业中心;布吉、龙岗、坂田、莲塘等中心的工作通勤流入量大于流出量;罗湖、龙华、布吉等跨区出行较多的中心,形成明显的集聚特征。此外,宝安北、横岗、平湖、石岩、盐田、光明、坪山等外围中心的工作通勤对称性最强,基本形成相对独立的新城,跨区出行比例较小(表2、图8)。
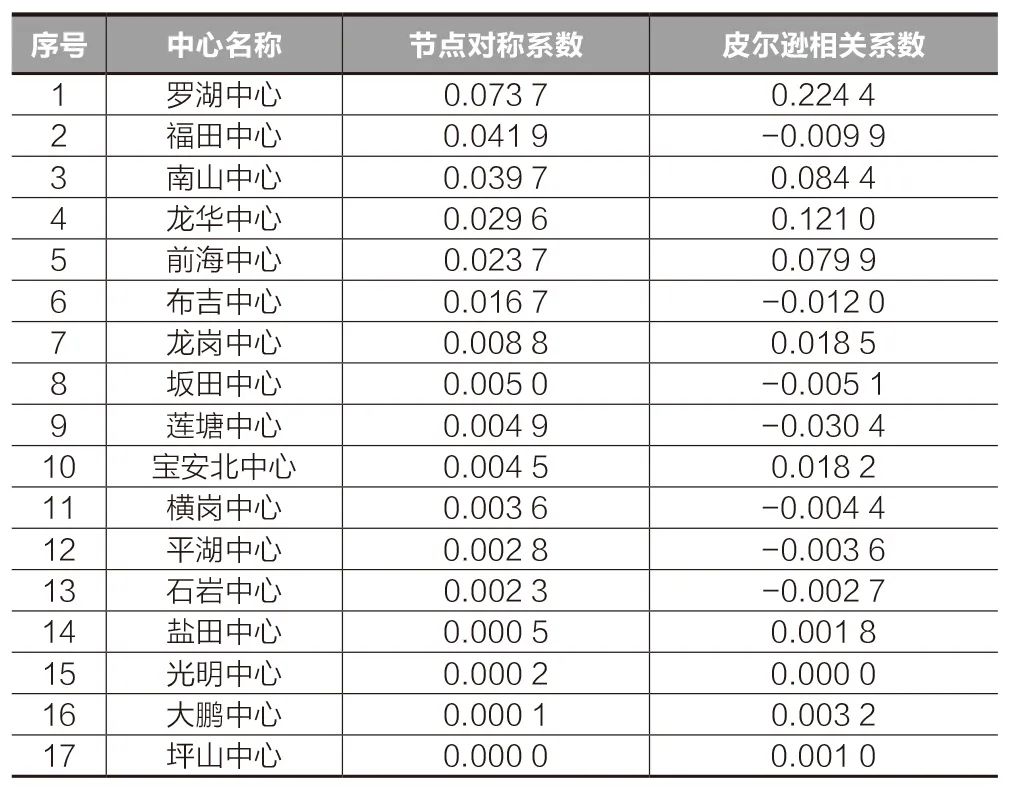
表2 各中心集聚水平测度结果
Tab.2 Measurement results of agglomeration level of each center
资料来源:笔者自绘
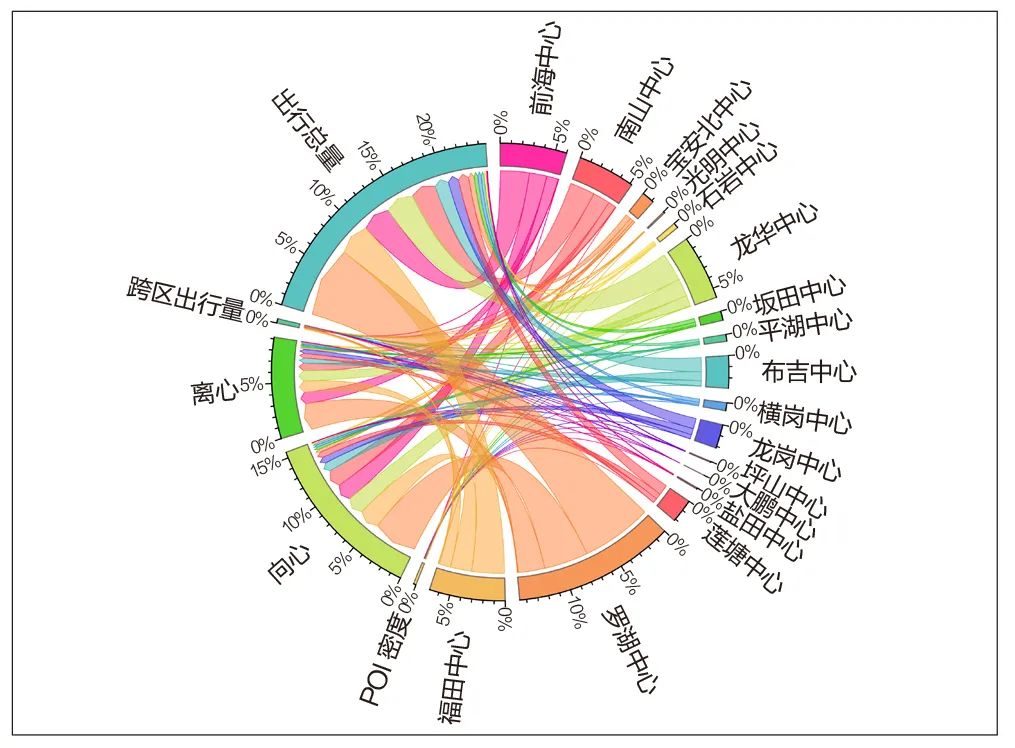
图8 各中心出行数量与POI密度数据统计弦图
Fig.8 Data statistics chord diagram of trips and POI density between centers
资料来源:笔者自绘
皮尔逊相关系数的测度结果表明:罗湖、龙华、南山、前海、龙岗、宝安北等中心的跨区出租车通勤与POI数量存在正相关关系,此类中心往往形成一定规模的服务功能,具有较强的集聚能力,是城市主要的就业中心;莲塘、布吉、坂田、横岗等中心的出租车跨区通勤与POI数量呈负相关关系,此类中心以居住功能为主,尚未形成较强的集聚能力,仍十分依赖周边中心的就业服务功能。
综合各中心的功能联系性、集聚水平指标,加权求和计算各中心的协同性。协同性最为突出的是罗湖、龙华、南山、前海和福田等中心;协同性较弱的中心主要包括光明、坪山、盐田、大鹏、石岩等,此类中心与其他中心的联系弱,多通过邻近的城市主中心与其他区域联系(表3)。
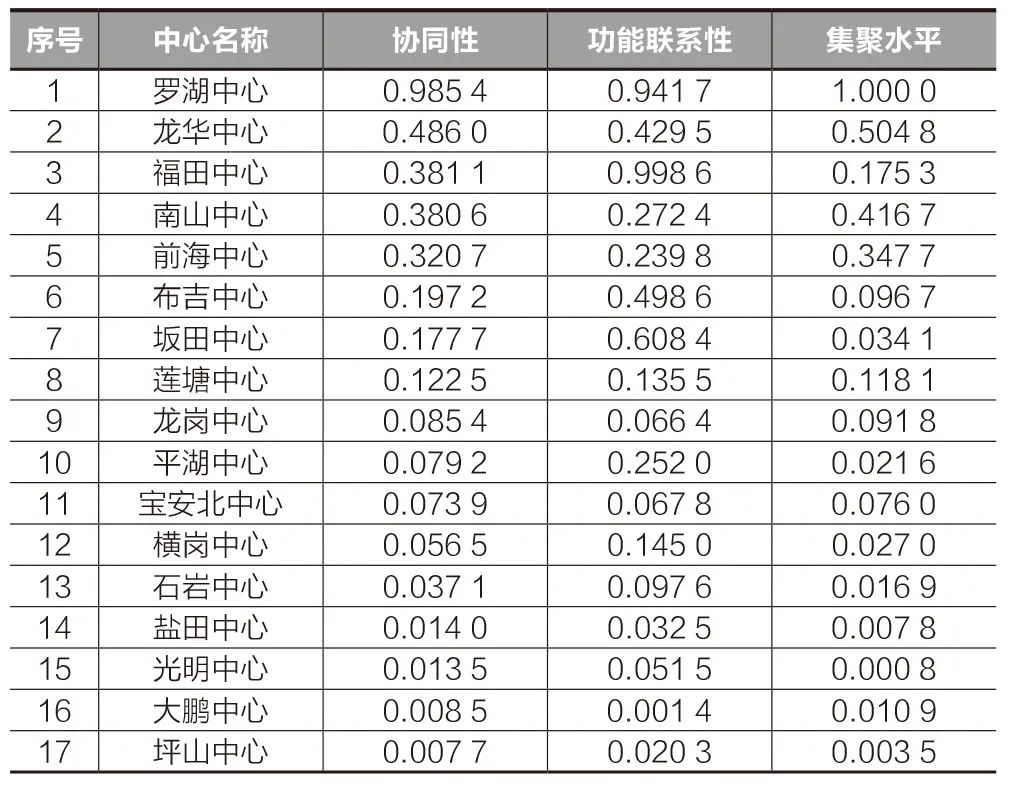
表3 各中心协同性测度结果
Tab.3 Synergy measurement results of each center
资料来源:笔者自绘
3.2 多中心空间结构的协同性分析
3.2.1 深圳市多中心空间结构协同性特征
从测度结果看,深圳市多中心空间结构已呈现网络化发展趋势。其特征表现为主要城市中心的集聚能力持续强化,外围组团的独立性不断加强,以及枢纽型节点的重要性增强等。
第一,协同性最为突出的中心,既包括罗湖、福田、南山、前海等政策重点倾斜的城市中心,也包括龙华等因地理区位优势形成的枢纽型中心。早期的罗湖商业中心,后来逐步建设的福田行政服务中心、南山综合服务中心及前海现代服务业中心,相继得到强化,体现规划引领的结果。但是,“十三五”期间,“东进”战略下的东部中心(龙岗中心)并未成型。而依托高铁枢纽形成的龙华中心却得到充分发展,主要原因包括三方面:其一,龙华地处深圳市的几何中心位置,是东西向、南北向联系的必经之地,是周边各中心联系的枢纽;其二,随着深圳北站和地铁4、5、6、10号线投入运营,龙华中心与周边各中心的交通联系得到充分强化;其三,龙华片区的主要功能仍以居住为主,但其南侧的罗湖、福田等中心是深圳市最大的就业中心,环龙华区域还分布着坂田、平湖、石岩、光明等以产业、科技为主要功能的就业中心,具备得天独厚的职住协同环境。
第二,光明、坪山、盐田、大鹏、石岩等中心的协同性较弱,体现深圳市2010年后转型发展的结果。一方面,东部的盐田、大鹏等区域,逐步向生态休闲、旅游服务功能转型,与其他城市功能片区的就业联系较弱;另一方面,随着深圳市战略性新兴产业、城市更新、强区放权等一系列改革措施的实施,外围组团发展的独立性有所强化,大量的产业园区在城市“退二进三”的过程中转型为新型产业功能区,形成诸多综合性的商务、商业中心。此外,罗湖、福田、南山等城市中心高昂的住房价格,也推动外围组团的居住功能发展,形成相对独立的城市功能区。
第三,枢纽型节点的重要性凸显。前海、石岩、龙华、坂田、布吉、平湖等中心已经成为南山、福田、罗湖等传统中心对外辐射的枢纽。在空间功能方面往往更加综合,这与外围的产业组团和中心区的总部办公、商业商务、行政服务功能有巨大的差异,是城市发展平台的主要集聚区,也是最具活力和发展潜力的地区。
总体而言,深圳市多中心城市空间结构的形成,有着复杂的历史原因和城市发展转型背景。从多中心城市向网络化城市演变的过程中,深圳市各中心的协同关系趋于圈层外延化,深圳市各中心的独立性得到加强,越来越像由众多城镇组成的城镇群。位于外围的独立组团,在粤港澳大湾区甚至更大区域内的产业协作网络中扮演着重要的角色。而处于传统中心(罗湖、福田、南山)与外围中心之间的新中心(前海、石岩、龙华、坂田、布吉、平湖等),则是支撑城市快速转型、实现跨越式增长的战略地区。
3.2.2 深圳市空间结构多中心化演变机理分析
从深圳市多中心城市空间结构的发展历程看,超大、特大城市是从单中心走向双中心、多中心,进而逐步演变为网络化结构。在这个过程中,原有城市中心的职能往往通过数次转型升级,强化对区域的带动辐射作用;而处于核心圈层边缘的新中心,往往能够迅速与原有城市中心形成良性的协同关系,成为城市转型发展的战略性区域;那些具备区位、交通和功能优势的区域,往往能够得到率先发展。随着,超大、特大城市规模的逐步扩大,城市往往形成多个内部功能完善的新城组团,从而降低对原有城市中心的依赖,并随着城市的逐步发展,形成新的全市性综合服务中心。在开放的市场资源配置网络中,某些专业性中心还可能成为区域乃至更大范围的综合服务枢纽,超大、特大城市的网络化结构越来越类似于城镇群。
值得注意的是,这种多中心结构与行政区划的关系。在城市外围中心的测度中,仍需要考虑与周边城镇节点的联系,囿于行政区划的测度结果,外围节点测度结果的偏差难以避免,将测度范围放大至深圳都市圈,仍会面临同样的问题。此外,经验和规划引导的城市空间结构与实际存在较大的差异,基于行政区划建构的城市中心体系,在经济高度发达的超大、特大城市中并不适用。类似坪山、大鹏、盐田等区级中心,在全市中心体系中的作用,远不及布吉、坂田、平湖、横岗等专业化职能中心。
04
结论与讨论
研究搭建的协同性测度框架,对超大、特大城市内部多中心空间结构的协同性测度具有积极的借鉴意义。通过功能联系性、集聚水平指标,测度各中心之间的联系、要素流动关系,评价各中心的集聚能力,进而测度多中心城市空间结构的协同性,是一种全面体现功能联系和空间集聚特征的综合测度方法。通过对深圳市多中心空间结构协同性的测度,得到如下结论:第一,深圳多中心空间结构已呈现网络化趋势,主要城市中心的集聚能力得到持续强化,外围组团的独立性有加强趋势,枢纽型节点的重要性逐步凸显;第二,罗湖、福田、南山、前海等城市级中心在政策引导下得到强化,龙华枢纽型综合服务中心也得到充分发展,而光明、坪山、盐田、大鹏、石岩等中心影响力较弱;第三,前海、石岩、龙华、坂田、布吉、平湖等中心表现为南山、福田、罗湖等传统中心对外辐射的枢纽。
但是,基于中心度、功能联系性和集聚水平指标的协同性测度,仍存在以下问题:一是测度范围问题,囿于行政区划的测度,会降低外围中心测度结果的准确性;二是样本的局限性,POI、出租车数据虽能在一定程度上反映城市各中心的协同关系,但仍存在大量居民通过公交、地铁、自驾等交通方式通勤,数据本身存在应用局限性。实践中,应结合可获取的数据对研究方法中的变量进行替换。



 立即订阅
立即订阅








